
Física del sonido
Naturaleza del sonido
El sonido consiste en la propagación de una perturbación en un medio (en general el aire).
¿Cómo es la energía sonora? ¿Cómo se propaga la energía de un lugar a otro?
Para comprender mejor esto imaginemos un tubo muy largo lleno de aire. El aire está formado por una cantidad muy grande de pequeñas partículas o moléculas. Inicialmente, el aire dentro del tubo está en reposo (o más técnicamente, en equilibrio). Este equilibrio es dinámico ya que las moléculas se mueven en todas direcciones debido a la agitación térmica, pero con la particularidad de que están homogéneamente distribuidas (en cada cm3 de aire hay aproximadamente la misma cantidad de moléculas - 25 trillones).
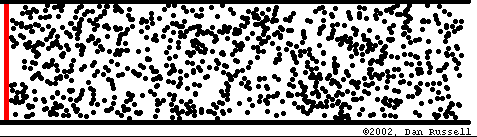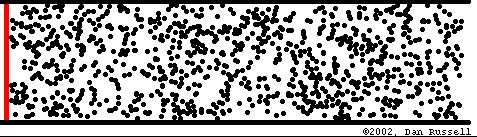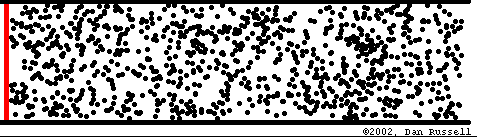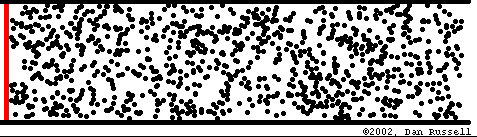
Supongamos que se mueve rápidamente el pistón hacia el interior del tubo. Las moléculas que se encuentran junto al pistón serán empujadas, mientras que las que se encuentran alejadas no. En la zona del pistón el aire se encontrará más comprimido que lejos de él, es decir que la misma cantidad de aire ocupa menos espacio. El aire comprimido tiende a descomprimirse (como cuando abrimos la válvula de un neumático) desplazándose hacia la derecha y comprimiendo el aire próximo. Esta nueva compresión implica nuevamente una tendencia a descomprimirse, por lo que la perturbación original se propaga a lo largo del tubo alejándose de la fuente.
Es importante enfatizar que el aire no se mueve de un lugar a otro junto con el sonido. Hay trasmisión de energía pero no traslado de materia (comparar con el olfato).
Propagación
Características del medio - Para que la onda sonora se propague en un medio este debe ser elástico, tener masa e inercia. El aire posee además algunas características relevantes para la propagación del sonido:
-
La propagación es lineal (en el intervalo de sonidos audibles la aproximación es válida). Esto permite que diferentes ondas sonoras se propaguen por el mismo espacio al mismo tiempo sin afectarse.
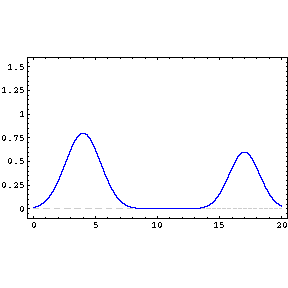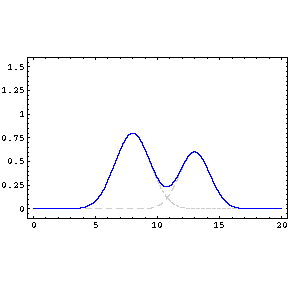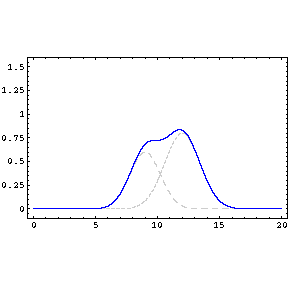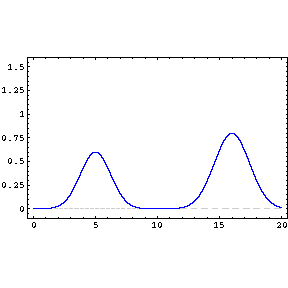
-
El medio es no dispersivo. Por esta razón las ondas se propagan a la misma velocidad independientemente de su frecuencia o amplitud.
-
El medio es homogéneo. No existen direcciones de propagación privilegiadas por lo que el sonido se propaga esféricamente (en todas direcciones).
Ondas Sonoras
Ondas Sonoras Periódicas
Si consideramos las expansiones y compresiones en un tubo acústico veremos que los desplazamientos del aire,respecto a su posición de equilibrio en cada punto, son en la direcci’on de propagación de la onda y están dados por:
s (x, t) = s mc o s (kx − ωt )
donde s m es el desplazamiento máximo del medio respecto a su posición de equilibrio(La amplitud de la onda). -Variación de la presión al pasar la onda: La definición del módulo volumétrico permite escribir:
∆ P = − B ∆ V/ Vi
Se tiene: Vi = A∆x ∆V = A∆s
Por lo tanto( en el lí mite ∆x − >d x) ∆P = −B ∂s∂x
Para una onda sinusoidal: ∆P = ρv2ksms e n(k x − ωt)
Intensidad de las ondas sonoras periódicas
Una onda transmite energía. La cantidad de energía por unidad de tiempo es la potencia transmitida por la onda. En MKS se mide en Watt.
La intensidad corresponde a una potencia distribuida en una superficie. I = P/A
La misma potencia se distribuye en 2 superficies distintas. Cambia la intensidad. PARA UNA FUENTE PUNTUAL SE USA UNA ESFERA: ¸ A = 4πR ^2
La energía mecánica total de una columna de aire de ancho dx es(A es la sección transversal del tubo): d E = 1 /2* ρAd x((∂s (x, t ) ∂t ) ^2 + ω ^2 s (x, t ) ^2 )
Esto es: d E = 1 /2 ρA d x s m ^2 ω ^2
La energía por unidad de tiempo(Potencia) es: P = 1 /2 ρA v s m ^2 ω ^2
La intensidad está dada por: I = P /A = 1 /2 ρvs m ^2 ω^ 2
En forma equivalente: I = ∆ Pm ^2/2ρv
Decibeles
Debido a la enorme sensibilidad del oí do humano, se mide el nivel sonoro β usando una escala logarítmica: β = 10log ( I /I0 )
donde I0 es la intensidad de referencia (el umbral auditivo=10 −12 W / m 2) e I es la intensidad en watts / m 2 . β se mide en decibeles (dB). El umbral auditivo corresponde a 0 decibeles. El límite del dolor a 120 decibeles
#include<iostream>
#include<math.h>
using namespace std;
double VEL(int T) ;
int Temp;
double R1,z;
int VP(int i , int o ) ;
double Vi,Vo,i,o,R2,z2,B=0.5;
double Int(double P , double A ) ;
int Pt,Am;
double z3,R3;
double Dec(int Ii,int Io );
double R4 , y , b ,z4 ;
int main()
{
int OPCION;
cout<<"ONDAS SONORAS\n ";
cout<<"*************\n ";
cout<<"MENU \n ";
cout<<"(1): Velocidad en cuanto a la temperatura \n ";
cout<<"(2): Variacion de la presion \n ";
cout<<"(3): Intensidad de onda \n ";
cout<<"(4): Decibeles \n ";
cout<<"INGRESE UNA OPCION: ";
cin>>OPCION;
switch(OPCION)
{
case 1:
{cin>>Temp;
R1=VEL(Temp);
cout<<R1<<endl;
};break;
case 2:
{cin>>Vo ; cin>>Vi ;
R2=VP(Vo,Vi);
cout<<R2<<endl;
};break;
case 3:
{cin>>Pt ; cin>>Am;
R3=Int(Pt,Am);
cout<<R3<<endl;
};break;
case 4:
{cin>>y ;cin>>b;
R4=Dec(y,o);
cout<<R4<<endl;
};break;
}
return 0;
}
//zona de funciones
double VEL(int T)
{
z=331*sqrt(1+(Temp/273));
return z;
}//FIN VEL
int VP(int i, int o )
{
z2=-B*(i/o);
return z2;
}//FIN VP
double Int(double P ,double A)
{
z3= P/A;
return z3;
}//FIN Int
double Dec(int Ii ,int Io )
{
z4=Ii/Io;
return z4;
}//FIN Aten